MINGGU |
BIDANG PEMBELAJARAN |
HASIL PEMBELAJARAN |
SUMBER/TEKNIK
/AKTIVITI |
| 1 - 3 |
Nombor
Bulat (Nombor bulat, Penambahan,
Penolakan,Pendaraban,Pembahagian, Prinsip Pengiraan cekap) |
| Aras 1 |
| Membilang objek dengan menyetakan dan menulis
nombor yang betul dengan angka dan perkataan |
| Menentukan nilai tempat bagi
sesuatu digit dalam suatu nombor |
| Membandingkan nombor berasaskan nilai tempat |
| Membundarkan nombor
kepada suatu nilai tempat tertentu |
| Menambah Nombor bulat |
| Menyelesaikan masalah yang
melibatkan penambahan nombor bulat. |
| Menolak satu Nombor Bulat daripada suatu
nombor bulat yang lebih besar atau sama |
| Menyelesaikan mesalah yang
melibatkan penambahan dan penolakan nombor bulat. |
| Mendarab nombor bulat |
| Menyelesaikan masalah yang
melibatkan pendaraban nombor bulat |
| Membahagi suatu nombor bulat dengan nombor
bulat yang lebih kecil daripadanya |
| Menyelesaikan masalah yang
melibatkan pendaraban dan pembahagian nombor bulat |
| Membina masalah perkataan berdasarkan situasi
harian yang melibatkan satu operasi |
| Membuat pengiraan yang
melibatkan beberapa operasi tambah dan tolak sahaja atau darab dan bahagi sahaja dari kiri
kekanan |
| Aras 2 |
| Membina masalah perkataan berdasarkan situasi
harian yang melibatkan dua operasi |
| Membuat pengiraan yang
melibatkan gabungan operasi tambah,tolak,darab dan bahagi mengikut tertib |
| Membuat pengiraan yang melibatkan tanda
kurung |
| Membuat pengiraan cekap
menggunakan pelbagai teknik |
| Aras 3 |
| Membina masalah perkataan berdasarkan situasi
harian yang melibatkan lebih daripada dua operasi . |
| Menyelesaikan masalah yang
melibatkan beberapa operasi termasuk tanda kurung |
| Membina dan mengemukakan keadah alternatif
untuk membuat pengiraan cekap |
|
Perkakasan teknologi,
perisian kursus,perisian apelakasi dan bahan bantu mengajar seperti kalkulator, carta
garis nombor, kad imbasan, batang cuisenaire dan permainanmatematik seperti dam ular,
" mathmagic", silang nombor digunakan untuk menegaskan kefahaman konsep nombor
bulat dan operasi yang berkaitan. Untuk membina masalah perkataan, maklumat atau konteks
sesuatu masalah itu diberi.
| (a) Contoh maklumat |
| i.Ayat matematik |
| 2 + 3 = 5 |
| ii Angka dan operasi: |
| 2,3, x |
| iii Satu nombor : 50 |
| (b) Contoh konteks |
| Berbantuk situasi harian seperti dijalan
raya, padang permainan,perhentian bas dan kantin sekolah. |
Dalam prinsip pengiraan,pendaraban dan/atau pembahagian dilakukan
dahalu dari kiri ke kanan sebelum penambahan dan/atau pengurangan.
Tanda kurung digunakan sebagai
| (a) Tatatanda bagi pengiraan yang mesti didahalukan |
| Contoh: 2(3+2)= 2(5) |
| (b) Tatanda untuk pendaraban |
| Contoh: 7(4) = 7 x 4 |
Antara teknik pengiraan cekap yang boleh digunakan ialah menyusun
semula nombor, pengiraan dengan jari menghafal sifir dan menkaji pola. |
| 4 - 6 |
Gandaan
dan Faktor (Senarai nombor berpola Nombor perdana, Gandaan Gandaan sepunya
Faktor, Faktor perdana, Faktor sepunya, Faktor sepunya terbesar, Gandaan sepunya terkecil) |
| Aras 1 |
| Menyatakan pola daripada suatu senarai nombor
yang diberi dan sebaliknya |
| Menentukan samada suatu
nombor ialah nombor perdana |
| Menyenaraikan gandaan suatu nombor |
| Menguji samada suatu nombor
adalah gandaan bagi nombor yang diberi |
| Mencari gandaan sepunya dan gandaan sepunya
terkecil(GSTK) bagi mana-mana dua nombor yang diberi. |
| Menentukan faktor dan faktor
perdana bagi suatu nombor yang diberi. |
| Menentukan samada suatu nombor ialah faktor
sepunya bagi dua nombor yang diberi |
| Mencari faktor sepunya dan
faktor sepunya terbesar(FSTB) bagi dua nombor yang diberi. |
| Aras 2 |
| Mencari gandaan sepunya GSTK dan GSTK bagi
mana-mana tiga nombor yang diberi |
| Mencari faktor sepunya bagi
tiga nombor yang diberi |
| Menentukan sama ada suatu nombor ialah faktor
sepunya dan FSTB bagi tiga nombor yang diberi. |
| Aras 3 |
| Mencari gandaan sepunya dan gandaan sepunya
terkecil bagi lebih dari tiga nombor |
| Mencari faktor sepunya dan
faktor sepunya terbesar bagi lebih daripada tiga nombor |
| Menyelesaikan masalah yang melibatkan gandaan
dan faktor. |
|
Perkakasan teknologi,
perisian kursus,perisian aplikasi dan bahan bantu mengajar seperti cuisennair ,kalkulator
dan permainan matematik digunakan untuk menegaskan kefahaman konsep gandaan dan faktor. Nombor
genap dan ganjil sebagai suatu senarai nombor masing-masing
Tegaskan suatu nombor ialah gandaan bagi nombor itu sendiri.
Cara-cara ringkas untuk menguji pembahagian oleh 2,3,4,5,8,9, dan 10 diperkenalkan.
Mencari GSTK dengan cara:
| a) menyenaraikan beberapa gandaan sepunya |
| b) pembahagian berulang dengan faktor-faktor sepunya. |
Mencari FSTB dengan cara: |
| a) menyenaraikan semua faktor sepunya |
| b) pembahagian berulang dengan faktor-faktor sepunya. |
|
| 7 - 9 |
Pecahan (Pecahan,Pecahan
setara, Nombor bercampur, Pecahan wajar dan tak wajar, Penambahan pecahan, Penolakkan
pecahan ,pendaraban pecahan, pembahagian pecahan) |
| Aras 1 |
| Menyebut dan menulis pecahan sebagai mewakili
suatu bahagain tertentu daripada keseluruhan |
| Menandakan dalam suatu
gambarajah bahagian yang mewakili suatu pecahan |
| Menyatakan nombor 1 dalam bentuk pecahan |
| Mengenal pasti pengangka dan
penyebut bagi setu pecahan |
| Menentukan pecahan yang setara dengan pecahan
yang diberi |
| Menentukan sama ada dua
pecahan yang diberi adalah setara |
| Membandingkan pecahan dengan menggunakan
konsep pecahan setara |
| Menukar suatu pecahan kepada
pecahan dalam sebutan yang terendah |
| Menulis nombor bercampur yang mewakili nilai
yang ditunjukkan dalam gambarajah dan sebaliknya. |
| Menandakan pecahan nombor
bercampur pada suatu garis nombor |
| Menentukan sama ada suatu pecahan adalah
pecahan wajar dan pecahan tak wajar, |
| Menukarkan pecahan tak wajar
kepada nombor bercampur atau nombor bulat dan sebaliknya. |
| Mencari pecahan setara bagi pecahan tak
wajar. |
| Melakukan operasi tambah dan
tolak keatas pecahan yang melibatkan : |
| i. penyebut sama: |
| ii. penyebut berbeza(gunakan
GSTK) |
| iii. pecahan dengan nombor
bulat; |
| iv. pecahan dengan nombor
bercampur. |
| Menyelesaikan masalah harian yang melibatkan
penambahan dan pegurangan pecahan |
| Mencari hasil darab nombor
bulat dengan pecahan secara penambahan berulang pecahan tersebut. |
| Menentukan hasil operasi daripada terhadap
sebahagian kumpulan objek dengan menggunakan gambarajah. |
| Mencari pecahan daripada
suatu pecahan yang lain dengan menggunakan bahagian yang dikehendaki dalam suatu
gambarajah. |
| Mencari hasil darab pecahan dengan nombor
bulat secara mendarab pengangka pecahan dengan nombor bulat. |
| Mencari hasil darab dua
pecahan secara mendarab penanagka dengan pengangka serta penyebut dengan penyebut |
| Mencari hasil darab pecahan dengan nombor
bulat atau pecahan dengan pecahan secara pemansuhan. |
| Membahagi suatu bahagian
tertentu daripada suatu keseluruhan kepada beberapa bahagian yang lebih kecil dan
mewakilkan bahagian kecil itu sebagai sebahagian daripada keseluruhan. |
| Mencari hasil bahagi suatu pecahan dengan
nombor bulat |
| Membahagi nombor dengan
pecahan secara mencari berapa kali pecahan tersebut terkandung dalam nombor itu secara
gambarajah. |
| Mencari hasil bahagi nombor bulat dengan
pecahan. |
| Aras 2 |
| Menambah dan/atau menolak dua dan tiga nombr
yang melibatkan pecahan dan/atau nombor bercampur |
| Menyelesaikan masalah yang
melibatkan penambahan dan penolakan pecahan. |
| Mencari hasildarab bagi dua nombor atau lebih
yang melibatkan pecahan dan/atau nombor bercampur dengan menukarkan nombor bercampur itu
kepada pecahan tak wajar dahalu. |
| Menyelesaikan masalah yang
melibatkan pendaraban pecahan |
| Mencari hasil bahagi pecahan dengan pecahan |
| Mencari hasil bahagi nombor
bercampur dengan menukarkan nombor bercampur itu kepada pecahan tak wajar dahalu. |
| Membuat pengiraan pendaraban dan/atau
pembahagian bagi tiga nombor atau lebih yang melibatkan pecahan dan/atau nombor bercampur. |
| Menyelesaikan masalah yang
melibatkan pembahagian pecahan. |
| Aras 3 |
| Menyelesaikan masalah yang melibatkan
pendaraban dan pembahagian pecahan |
| Membuat pengiraan yang
melibatkan beberapa operasi termasuk penggunaan tanda kurung bagi kombinasi nombor bulat,
pecahan dan nombor bercampur. |
|
Perkakasan teknologi,
perisian kursus,perisian aplikasi dan bahan bantu mengajar seperti model dan carta pecahan
digunakan untuk menegaskan kefahaman konsep pecahan dan operasi ke atasnya. Hanya
perwakilan bagi pecahan wajar sahaja digunakan bagi memperkenalkan konsep pecahan .
Kesamaan saiz antara setiap bahagian dalam satu keseluruhan mesti ditegaskan.
| (a) per dalam pecahan bermaksud bahagi |
| (b) Penggunaan daripada dalam konteks berikut
bermaksud pendaraban |
| Penggunaan model atau gambarajah untuk memperkenalkan
konsep pendaraban dan pembahagian perlu dikaitkan dengan algoritma perasi berkenaan. |
| Contoh untuk membahagi dan mewakilkan suatu bahagian
daripada satu keseluruhan: |
| Bagi mencari hasil bahagi pecahan dengan nombor bulat,
antara cara yang boleh digunakan |
| Bagi membahagi nombor dengan pecahan, secara gambarajah
gunakan |
| Aktiviti membina cerita berdasarkan situiasi harian yang
melibatkan pecahan untuk memperkukuhkan kefahaman konsep pecahan diperkenalkan. |
|
| 10 - 12 |
Nombor
Perpuluhan (Penambahan Nombor perpuluhan, Penolakan Nombor perpuluhan,
Pendaraban Nombor perpuluhan ,Pembahagian Nombor perpuluhan) |
| Aras 1 |
| Menukar pecahan yang penyebutnya kuasa 10
sebagai nombor perpuluhan dan sebaliknya |
| Menukar pecahan kepada nombor
perpuluhan hingga empat tempat perpuluhan tertentu dan sebaliknya |
| Menentukan nilai tempat bagi suatu digit
dalam suatu nombor perpuluhan. |
| Membandingkan nombor
perpuluhan berdasarkan nilai tempat |
| Membuat pengiraan yang melibatkan operasi
tambah bagi nombor perpuluhan dengan nombor bulat dan nombor perpuluhan dengan nombor
perpuluhan |
| Membuat pengiraan yang
melibatkan operasi tolak bagi nombor perpuluhan dengan nombor bulat dan nombor perpuluhan
dengan nombor perpuluhan |
| Menyelesaikan masalah harian yang melibatkan
tambah atau tolak bagi nombor perpuluhan dengan nombor bulat dan nombor perpuluhan dengan
nombor perpuluhan |
| Membuat pengiraan yang
melibatkan operasi darab bagi nombor perpuluhan dengan nombor bulat dan nombor perpuluhan
dengan nombor perpuluhan |
| Membuat pengiraan yang melibatkan operasi
bahagi bagi nombor perpuluhan dengan nombor bulat dan nombor perpuluhan dengan nombor
perpuluhan |
| Menyelesaikan masalah harian
yang melibatkan darab atau bahagi bagi nombor perpuluhan dengan nombor bulat dan nombor
perpuluhan dengan nombor perpuluhan |
| Aras 2 |
| Membuat pengiraan yang melibatkan gabungan
operasi tambah atau tolak bagi kombanasi nombor perpuluhan dengan nombor bulat |
| Membuat pengiraan yang
melibatkan gabungan operasi darab atau bahagi bagi kombanasi nombor perpuluhan dengan
nombor bulat |
| Menyelesaikan masalah harian yang melibatkan
gabungan dua operasi tambah,tolak, darab atau bahagi. |
| Aras 3 |
| Membuat pengiraan yang melibatkan gabungan
operasi darab atau bahagi nombor perpuluhan dengan pecahan |
| Menyelesaikan masalah yang
melibatkan gabungan operasi darab atau bahagi nombor perpuluhan dengan pecahan |
|
Perkakasan teknologi,
perisian kursus,perisian aplikasi dan bahan bantu mengajar seperti blok beganda dan model
garisan nombor digunakan untuk menegaskan konsep nombor perpulahan dan operasi ke
atasnya.Kalkulator digunakan untuk menunjukkan perkaitan antara pecahan dengan perpuluhan.
Fokus pengajaran kepada perkaitan tersebut dan bukan kepada pengiraan rumit. Perlu
ditegaskan nombor perpuluhan sebagai mewakili pecahan yang penyebutnya kuasa 10 iaitu
10,100,1000 dan seterusnya.
Bagi operasi tambah dan operasi tolak, pengiraan boleh dilakukan dengan menyusun
titik-titik perpuluhan pada garis tegak.
Pengiraan tepat sehingga 4 tempat perpuluhan sahaja
Untuk memperkenalkan cara menentukan tempat titik perpuluhan bagi hasil darab dua
nombor perpuluhan,pendekatan berikut boleh digunakan:
| (a)Membuat anggaran jawapan |
| Contoh : |
| Hasil darab 2.7 dengan 30.75 mestilah dalam lingkungan 90
kerana 3 didarab 30 adalah 90 |
| (b) Merujuk nilai tempat terkecil Contoh : |
| (c) Menukar perpuluhan kepada pecahan,mendarab pecahan
yang diperoleh dan menukar semula kepada nombor perpuluhan untuk menunjukkan kaitan antara
bilangan tempat perpuluhan dalam perpuluhan didarab dengan bilangan tempat perpuluhan
dalam hasil darab. |
|
| 13 - 15 |
Peratus |
| Aras 1 |
| Menulis suatu pecahan wajar dengan penyebut
100 dalam peratus dengan menggunakan simbol % dan sebaliknya |
| Menukar sebarang pecahan
kepada peratus dengan mendarab pecahan dengan 100% |
| Menulis sebahagian daripada suatu nilai
sebagai peratusan |
| Mencari nilai keseluruhan
apabila nilai sebahagiannya dan peratusan bahagian tersebut diberi. |
| Aras 2 |
| Mencari nilai tambahan, nilai susutan dan
nilai akhir selepas tambahan atau susutan sebanyak suatu peratusan tertentu |
| Mencari tambahan atau susutan
dalam peratusan apabila berlaku perubahan pada nilai asal |
| Mencari nilai asal apabila peratus perubahan
dan nilai akhir diberi |
| Menyelesaikan masalah harian
yang melibatkan peratus. |
|
Perkakasan teknologi,
perisian kursus,perisian aplikasi dan bahan bantu mengajar seperti keratan akhbar dan
risalah bank digunakan untuk menegaskan kefahaman konsep peratus. Tegaskan bahawa
seratus peratus suatu nilai ialah nilai itu sendiri.
Tunjukkan bahawa peratus boleh digunakan untuk membandingkan dua situasi
Menjalankan projek tertentu yang membolehkan pelajar mengaplikasi peratus dalam membuat
keputusan atau kesimpulan.
Bagi penyelesaian masalah harian libatkan penggunaan peratus kepada untung, rugi,faedah
ringkas,dividen,komisen dan diskaun. |
| 16 |
Peperiksaan
Pertengahan Tahun |
|
|
| 17 - 19 |
Integer
dan Nombor Negatif (1) ( Nombor negatif, Integer, Integer positif, Integer
negatif, Tertib integer, penambaahn integer) |
| Aras 1 |
| Menggunakan nombor positif atau negatif untuk
mewakili situasi harian yang melibatkan nilai yang bertambah atau berkurang nilai yang
lebih daripada sifir atau kurang daripada sifar |
| Menentukan sama ada suatau
nombor ialah integer atau tidak |
| Menentukan sama ada suatau nombor ialah
integer positif atau integer negatif |
| Mewakili integer positif dan
integer negatif pada garis nombor. |
| Menyatakan nombor yang lebih besar atau lebih
kecil jika diberi dua integer |
| Menyusun beberapa integer
mengikut tertib menaik atau menurun |
| Menentukan integer yang terbesar atau
terkecil antara beberapa integer yang diberi |
| Aras 2 |
| Menentukan beberapa integer yang tidak
diberikan suatu senarai integer berpola |
| Manambah dua integer atau
tiga integer |
| Menolak antara dua integer |
| Mempermudahkan dan mencari
hasiltambah atau hasil tolak antara dua integer. |
| Menambah dan menolak sebarang tiga integer |
| Menyelesaikan masalah yang
melibatkan penambahan dua atau tiga integer |
| Menyelesaikan masalah yang melibatkan
penolakkan antara dua integer |
| Menyelesaikan masalah harian
yang melibatkan penambahan dan penolakkan antara dua integer |
| Aras 3 |
| Menentukan penambahan dengan integer nagatif
memberi hasil yang sama dengan penolakkan dengan nombor bulat. |
|
Perkakasan teknologi,
perisian kursus,perisian aplikasi dan bahan bantu mengajar seperti carta garis nombor, cip
warna dan temormetor digunakan untuk menegaskan konsep nombor negatif. Tegaskan nombor
negtif sebagai nombor yang digunakan dalam setuasi tertentu: tanda (-) digunakan untu
menunjukkan satu sifat selain magnitud
Contoh : arah
Tegaskan integer sebagai nombor bulat yang mempunyai tanda positif atau
negatif,termasuk sifar
Integer positif sebagai nombor bulat dengan tanda (+) atau tanpa tanda
Integer negatif sebagai nombor bulat dengan tanda (-)
Perkenalkan konsep dengan aktiviti
Model garis nombor dan benda maujud boleh digunakan untuk proses penambahan atau
penolakkan integar
Kegunaan kurungan ditegaskan bagi penambahan yang melibatkan integer negatif
Tegaskan perbezaan penggunaan ' - ' sebagai suatu operasi atau tanda bagi nombor dan
perbezaan sebutannya
Masalah berkaitan penambahan dan penolakkan merangkumi bentuk
Tegaskan perbezaan antara integer negatif dan operasi tolak |
| 20 - 22 |
Ukuran Asas (Ukuran Panjang, Unit Ukuran panjang,Penanggaran,jisim,Masa dan waktu |
| Aras 1 |
| Mengukur Panjang jisim dan masa dalam unit
arbitari. |
| Mengukur panjang dalam unit
metrik. |
| Mengnggar jarak atau panjang dalam unit
metrik yang sesuai. |
| Menukar ukuran panjang
daripada suatu unit kepada unit yanglain |
| Menyelesaikan masalah ukuran panjang yang
melibat operasi tambah,tolak,darab,bahagi. |
| Mengukur jisim dalam unit
metrik. |
| Menganggar jisim suatu objek menggunakan unit
metrik yang sesuai |
| Menukar unit jisim daripada
suatu unit kepada suatu unit yang lain antara g , kg, tonne |
| Menyelesaikan masalah ukuran jisim yang
melibatkan operasi tambah, tolak, darab bahagi |
| Mengukur masa suatu aktiviti
dalam saat,minit dan jam |
| Meanggar masa dalam unit yang sesuai |
| Menukar ukuran masa daripada
suatu unit kepada unit yang lain |
| Menyelesaikan masalah yang melibatkan operasi
tambah tolak darab bahagi. |
| Menyatakan waktu menggunakan
sistem 12 jam dan 24 jam |
| Menukar waktu sistem 12 jam kepada sestem 24
jam dan sebaliknya |
| Menentukan tempoh masa antara
dua waktu yang diberi |
| Menyelesaikan masalah harian yang melibatkan
masa dan waktu. |
| Aras 2 |
| Menyelesaikan masalah harian yang melibatkan
jisim atau masa |
| Aras 3 |
| Membina masalah perkataan yang melibatkan
ukuran asas berdasarkan konteks yang diberi |
|
Perkakasan teknologi,
perisian kursus,perisian aplikasi dan bahan bantu mengajar seperti pembaris,benang pita
ukur, kayu panjang ,jam randik jam tangan dan alat timbang digunakan untuk menegaskan
kefahaman konsep ukuran asas. Ukuran asas digunakan dengan menggunakan unit abritari
seperti sepelaung,sejangkal.
Bagi ukuran panjang libatkan garisan lurus dan lengkung
Unit ukuran panjang ialah mm,cm,m,km
Unit ukuran jisim ialah g,kg,tonne
Unit ukuran masa ialah saat,minit,jam hari minggu bulan dan tahun
Untuk meningkatkan kefahaman dalam ukuran asas aktiviti luar kelas atau projek perlu
diadakan
Menjalankan dan membentangkan hasil projek - mencipta suatu objek yang melibatkan
ukuran asas contoh pembinaan rangka bernbentuk kubus, ukuran asas yang terlibat ialah
panjang sisi kubus jisim kubus dan tempuh masa untuk menyiapkan projek.
Perbandingan sistem matrik dengan sestem bukan matriks dibincangkan. |
| 23 - 25 |
Sudut dan
Garis Selari (Sudut,Unit ukuran sudut, Putaran lengkap, Sudut tegak, Sudut
tirus, Sudut cakah, Sudut refleks,Garis yang bersilang, Garis selari,Sifat-sifat sudut
berkaitan dengan garis selari) |
| Aras 1 |
Menandakan dan menamakan sudut bagi suatu
putaran dengan menggunakan tatatanda seperti Ð BAC, Ð A, A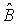 C. C. |
| Mengukur suatu sudut yang
diberi menggunakan protractor |
| Melukis suatu sudut yang diberi ukurannya |
| Menyatakan satu putaran
lengkap sebagai sudut 360 |
| Menyatakan pecahan suatu putaran lengkap
sebagai sudut dalam darjah dan sebaliknya |
| Menyatakan suku putaran
lengkap sebagai sudut tegak |
| Menyetakan saiz sudut tegak dalam darjah |
| Menentukan sudut yang diberi
samada sudut tirus,tegak, cakah atau sudut refeleks |
| Menyatakan hasiltambah sudut-sudut pada satu
garis lurus |
| Mencari nilai sudut pada
garislurus dengan diberi sudut yang lain |
| Menyatakan hasil tambah sudut pada suatu
titik |
| Mencari satu daripada
beberapa sudut pada suatu titik jika diberi sudut yang lain |
| Menyatakan samada suatu garis adalah garis
serenjang kepada suatu garis yang lain atau tidak |
| Melukis garis serenjang
kepada suatu garis lurus |
| i) pada suatu titik di atas
garis itu |
| ii)dari suatu titik yang
bukan di atas garis itu |
| Mengukur jarak tegak dari suatu titik ke
suatu garis lurus |
| Mencari suatu sudut,apabila
sudut-sudut bersebelahannya pada suatu garis lurus diberi. |
| Menandakan sudut-sudut bertentangan bucu bagi
dua garis lurus yang bersilang |
| Menamakan sudut-sudut yang
sama, diberi dua garis lurus yang bersilang |
| Menentukan nilai sudut pada titik persilangan
dua garis lurus, jika sebarang satu sudut diberi. |
| Menyatakan samada dua garis
yang biberi selari atau tidak |
| Melukis garis selari dengan suatu garis yang
diberi |
| Menentukan rentasan lintang
dalam gambarajah yang melibatkan garis selari |
| Menyatakan sudut sepadan berkaitan dengan
garis selari yang diberi |
| Mencari sudut sepadan dengan
sudut yang diberi |
| Menyatakan sudut selang seli bagi garis
selari yang diberi |
| Mencari suatu sudut diberi
sudut berselang seli padanya |
| Menentukan sudut-sudut pedalaman bagi dua
garis selari yang diberi |
| Mencari satu sudut daripada
sudut-sudut pedalaman berkaitan dengan dua garis selari diberi sudut pedalaman yang lain. |
| Aras 2 |
| Menentukan samada dua garis lurus yang
diberikan adalah selari atau tidak dengan |
| i)mengukur sudut sepadan; |
| ii) mencari nilai sudut sepadan diberi
sudut-sudut tertentu |
| iii) mengukur sudut selang seli |
| iv) mencari nilai sudut selang seli |
| v)mencari hasiltambah sudut pedalaman |
| Mencari sebarang sudut
berkaitan dengan garis selari diberi sudut-sudut tertentu |
| Aras 3 |
| Membukti sifat-sifat sudut berkaitan dengan
garis selari |
| Membina masalah yang
melibatkan pelbagai jenis sudut dan garis selari. |
|
Perkakasan teknologi,
perisian kursus,perisian aplikasi seperti geometer sketchpad dan bahan bantu mengajar
seperti sesiku,protrraktor, pembaris dan gambar objek untuk menegaskan kefahaman konsep
sudut dan garis selari serta aktiviti pengajaran dan pembelajaran. Tegaskan penggunaan
protraktor dengan cara yang betul.
Sudut juga boleh ditunjukkan melalui aktiviti lipatan kertas.
Kaitkan dengan sudut yang terdapat dalam alam sekeliling |
| 27 - 29 |
Poligon
(1) (Poligon, bucu,pepenjuru Semetri, Segitiga ,Segitiga sama sisi,
Segitiga sama kaki. Segitiga tak sama kaki,Segitiga bersudut tirus, Segitiga
bersudut cakah, Segitiga bersudut tegak, Sisiempat, Segiempat tepat, Segiempat
sama,Segiempat selari,Rombus dan Traperizum) |
| Aras 1 |
| Menamakan suatu poligon yang diberikan |
| Menentukan bilangan sisi,
bucu dan pepenjuru dalam suatu pligon yang diberikan |
| Melakar poligon |
| Menentukan samada objek yang
diberi mempunyai semetri garis atau tidak |
| Menentukan paksi semetri suatu objek yang
mempunyai simetri garis |
| Melengkapkan pola, diberikan
paksi semetri dan sebahagian pola |
| Menyatakan sama ada suatu bentuk (2 matra)
itu segitiga atau tidak |
| Menyatakan jenis segitiga
apabila diberi suatu segitiga tertentu |
| Mencari paksi semetri bagi suatu segitiga
jika ada. |
| Melukis suatu segitiga
tertentu |
| Menyatakan hasil tambah sudut-sudut sudut
pedalaman segitiga ialah 180 0 |
| Menyatakan semua sudut
pedalaman suatu segitiga sama sisi adalah sama besar dan bernilai 600. |
| Menyatakan dua sudut yang bertentangan dengan
dua sisi yang sama panjang dalam suatu segitiga sama kaki adalah sama besar. |
| Mencari nilai satu sudut
dalam segitiga jika diberikan maklumat yang mencukupi bagi sudut yang lain. |
| Menentukan sama ada suatu segitiga adalah
segitigasama kaki atau segitiga sama sisi dengan melihat sudut. |
| Menentukan sudut peluaran
pada suatu bucu segitiga |
| Menyatakan bahawa sudut peluaran sama dengan
hasil tambah sudut pedalamam bertentangan. |
| Menyatakan sama ada bentuk
(2-matra) ialah segiempat atau tidak. |
| Menyatakan jenis sisiempat apabila diberikan
suatu sisi empat tertentu. |
| Mencari paksi semetri bagi
suatu sisiempat tertentu |
| Menyatakan hasil tambah sudut-sudut sudut
pedalaman suatu sisiempat ialah 360 0 . |
| Menyatakan bahawa setiap
pasang sudut yang bertentangan dalam segiempat selari adalah sama besar. |
| Aras 2 |
| Membuat sebarang pola, diberika paksi semetri |
| Mengira salah satu sudut
Peluaran dan sudut pedalaman bertentangan jika diberi dua sudut yang lain |
| Mencari nilai satu sudut dalam sisiempat jika
diberikan maklumat yang mencukupi |
| Aras 3 |
| Menentukan hasil tambah sudut-sudut pedalamam
bagi pentagon, heksagon,heptagon dan oktagon |
| Merumus perkaitan di antara
bilangan sisi dengan jumlah sudut-sudut pedalaman bagi suatu poligon |
| Membuktikan sifat-sifat sudut berkaitan
dengan poligon |
|
Perkakasan teknologi,
perisian kursus,perisian aplikasi seperti geometer sketchpad dan bahan bantu mengajar
seperti origami pembaris, kertas grid batik dan gambar seni bina bangunan digunakan untuk
menegaskan kefahaman konsep poligon serta menyemai nilai-nilai seni. Bagi melengkapkan
pola, projek atau penyediaan folio diadakan untuk menghasilkan corak yang kreatif.
Menjalankan projek atau aktiviti yang melibatkan binaan.
Bagi membuat sebarang pola, projek atau penyediaan folio di
adakan untuk menghasilkan corak yang kreatif
Menyediakan folio mengenai kewujudan bentuk poligon disekililing kita seperti dalam
a) alam semula jadi
b) bidang seni bina. |
| 30 - 33 |
Perimeter dan
luas (Perimeter, luas , tinggi) |
| Aras 1 |
| Menyatakan perimeter sebagai ukuran panjang
sekeliling suatu kawasan |
| Mengukur perimeter bagi
bentuk dua matra |
| Mengira perimeter poligon dalam unit metrik |
| Menyelesaikan masalah yang
melibatkan perimeter |
| Menyatakan luas sebagai ukuran saiz suatu
kawasan |
| Mengukur luas suatu kawasan
secara membilang beberapakali suatu bentuk kecil (tidak semestinya segiempat sama) boleh
menutupi kawasan itu dengan lengkapnya |
| Menyatakan luas segiempat sama yang sisinya 1
unit ialah 1 unit 2 . |
| Menentukan luas sebarang
bentuk dengan membilang petak segiempat sama unit dalamnya |
| Mengira luas bagi suatu segiempat tepat dalam
cm2, m2,km2, dengan menggunakan rumus |
| Mengira luas segitiga
bersudut tegak |
| Mengira luas bentuk cantuman yang mengandungi
segiempat tepat dan segitiga bersudut tegak |
| Aras 2 |
| Meanggar luas suatu kawasan dengan meanggar
dulu panjang dan lebarnya |
| Menukar daripada suatu unit
kepada unit yang lain antara mm 2, cm2,m2, dan ha(hektar) |
| Menentukan tinggi suatu bentuk bagi tapak
yang berlainan |
| Mencari luas segitiga,
segiempat selari,trapezium. |
| Mencari panjang satu sisi atau tinggi suatu
bentuk, diberi luas dan sisi yang lain. |
| Mencari luas bentuk cantuman
yang terdiri daripada segitiga, segiempat selari dan trepezium |
| Mencari luas bahagian yang tertinggal selepas
bentuk segitiga, segiempat selari atau trapezium dikeluarkan daripada suatu bentuk yang
diberikan |
| Menyelesaikan masalah
melibatkan luas |
| Menyelesaikan masalah yang melibatkan luas
dan perimeter |
| Aras 3 |
| Membuktikan rumus luas sebarang segitiga |
| =1/2 (panjang tapak x tinggi) |
| Membuktikan rumus luas
trapezium |
| = 1/2 (jumlah sisi selari)(jarak antara 2
sisi selari) |
|
Perkakasan teknologi,
perisian kursus,perisian aplikasi seperti geometer sketchpad dan bahan bantu mengajar
seperti kertas surih,kertas graf,papan geometri, blok geometri dan objek-objek sebenar
digunakan untuk menegaskan kefahaman konsep primeter dan luas Untuk mencari luas suatu
objek, konsep tinggi objek perlu ditegaskan.
Bagi mengira luas seatu segiempat tepat rumas luas segiempat tepat = panjang x lebar
diterbitkan dengan membilang segiempat sama unit dalam segiempat tepat.
Rumus luas segitiga bersudut tegak = 1/2 x luas segiempat tepat diperkenalkan.
Bagi penyelesaian masalah , cantuman bentuk -bentuk objek perlu
ditegaskan. Hubungkait bentuk-bentuk objek yang dilukis berdasarkan perimeter atau luas
yang diberi juga perlu dibincangkan.
Contoh:
a) Primeter bagi segiempat tepat = 20 cm |
| 34 - 37 |
Pepejal dan
Isipadu (I) (Pepejal ,kubus) |
| Aras 1 |
| menamakan pepejal
kubus,kuboid,prisma,silinder,piramid,kon dan sfera., |
| Menentukan bilangan muka,tepi
dan bucu pada kubus dan kuboid. |
| Menyatakan ciri-ciri berkaitan dengan
muka,tepi dan bucu bagi kuboid dan kubus. |
| Membina kubus dan kuboid : |
| i) dengan mencantumkan enam
mukanya |
| ii) melalui pembinaan
bentangannya |
| Mewakili kubus dan kuboid sebagai lukisan
2-matra pada : |
| i) kertas grid segiempat sama; |
| ii) kertas kosong. |
| Menyatakan samaada suatu
pepejal adalah prisma atau tidak dan sama ada suatu prisma tegak atau tidak |
| mewakilkan prisma sebagai lukisan dua matra
pada : |
| i) kertas grid segiempat sama; |
| ii) kertas kosong |
| Melakar bentuk keratan rentas
sesuatu prisma |
| Menyatakan isipadu kuboid dengan membilang
beberapa kubus unit diperlukan untuk mengisi kuboid itu |
| Menerbitkan rumus isipadu
kuboid |
| Mengira isipadu kuboid dalam mm3,cm3 atau
m3,diberi panjang, lebar dan tinggi. |
| Mengira salah satu daripada
panjang,lebar atau tinggi kuboid apabila diberi dua yang lain serta isipadunga. |
| Mengira isipadu prisma tegak berkeratan
rentas segitiga bersudut tegak sebagai setengah isipadu kuboid |
| Menerbitkan rumus isipadu
prisma tegak |
| Mengira isipadu prisma tegak berkeratan
rentas: |
| i) Segitiga |
| ii) Segiempat selari |
| iii) Trapezium |
| Menukar daripada satu unit
kepada yang lain antara mm3 cm3 ,m3 |
| Menukar daripada satu unit kepada yang lain
antara l ,ml,cm3 |
| Aras 2 |
| Mengira isipadu bahan cecair dalam bekas
berbentuk kuboid atau prisma tegak dengan menggunakan unit l ml |
| Mencari hasiltambah,
hasiltolak,hasildarab atau hasil bahagi yang melibatkan isipadu |
| Menyelesaikan masalah yang melibatkan
isipadu. |
| Aras 3 |
| Mencari isipadu bagi gabungan pepejal |
| Mencari jumlah luas permukaan
kubus dan kuboid. |
|
Perkakasan teknologi,
perisian kursus,perisian aplikasi seperti geometer sketchpad dan bahan bantu mengajar
seperti kertas surih,kertas graf,papan geometri, blok geometri dan objek-objek sebenar
digunakan untuk menegaskan konsep pepejal dan isipadu. Tegaskan isipadu kubus yang
tepinya 1 unit ialah 1 unit3 |
| 38- 39 |
Latih Tubi |
|
|
| 40 - 41 |
Peperiksaan
Akhir Tahun |
|
|